[Vol. 2] Capítulo 02 - Função exponencial

 1.0 Potenciação e radiciação

1.1 Potência com expoente natural

Sendo a um número real e n um número natural, n ≥ 2, definimos a potência de base a e expoente n como o produto dos n fatores iguais a.

    Além disso: 

    Exemplos:

1.2 Potência com expoente inteiro

    Sendo a um número real não nulo (a ≠ 0) e n um número inteiro positivo, define-se: 

Exemplo:

1.3 Propriedades da potenciação

1.5 Notação científica

    Sendo a um número real, tal que 1 ≤ a < 10,  e n um número inteiro, a forma em notação científica de um número real não nulo é dada por:

Exemplos:

    O raio médio do Sol é de aproximadamente 696.000.000 metros; em notação científica, temos:

696.000.000 metros =   (note que n = 6 e a = 6,96)

    O diâmetro do átomo de hidrogênio é de aproximadamente 0,0000000001 metro; em notação científica, temos: 0,0000000001 metro =   (note que n = 10 e a  = 1)

1.6 Radiciação

    Sendo a um número real não negativo e n um número natural não nulo, a raiz enésima de a é o número real não negativo b tal que . Em símbolos, podemos escrever: 

1.6.1 Propriedades de radiciação

1.7 Potência com expoente racional

    Se a é um número real positivo, m inteiro e n natural não nulo, define-se:

    Exemplos: 

OBS.: Para potências com expoente racional valem as mesmas propriedades das potências com expoentes inteiros

1.8 Atividades resolvidas

Questões

2.0 Função exponencial

    A função   dada por  , com a ∈ R, a > 0 e a ≠ 1, é denominada função exponencial de base a.

    Exemplos: 

2.1 Gráfico da função exponencial

1º caso: a > 1

    Esboço do gráfico da função  

    De maneira geral, quanto maior o valor do expoente x, maior é a potência , ou seja, se a > 1, a função f(x) =   é crescente em todo o seu domínio (quando o valor de x cresce, o valor de  também cresce).

2º caso: 0 < a < 1

Esboço do gráfico da função  

    De maneira geral, quanto maior o valor do expoente x, menor é a potência , ou seja, se 0 < a < 1, a função f(x) =  é decrescente em todo o seu domínio (quando o valor de x cresce, o valor de decresce).

2.2 Domínio, contradomínio, conjunto imagem de uma função exponencial

    A partir da definição da função exponencial, dada por f(x) =  (com a > 0 e a ≠ 1) e da observação dos dois gráficos, temos:

• o domínio da função exponencial dada por f(x) =  é D(f) = R;

• o contradomínio da função exponencial dada por f(x) =  é CD(f) = ;

• o conjunto imagem da função exponencial dada por f(x) =  é Im(f) = .

2.3 O número de Euler

    O número e, conhecido como número de Euler, é um número irracional cujo valor é 2,718281... Leonhard Euler (1707-1783) adotou a letra e para representar a constante em 1736 em uma de suas obras.

    O matemático John Napier (1550-1617) desenvolveu diversos trabalhos envolvendo esse número e, por isso, também é conhecido como número de Napier.

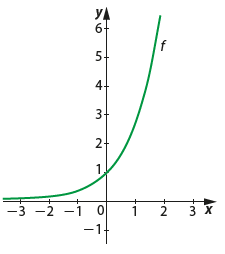
2.4 A função 

    É uma função exponencial cuja base é o número e. Vejamos o gráfico dessa função:

2.5 Atividades resolvidas 

Questões

3.0 Equação exponencial

    É toda equação cuja incógnita está no expoente de pelo menos uma potência de base real, positiva e diferente de 1. 

Ex.: 

    Para resolver equações exponenciais, é necessário representar ambos os lados da igualdade como potências de mesma base. Se as bases são iguais, o expoentes também serão iguais.

4.0 Inequação exponencial

    É toda desigualdade que apresenta incógnita no expoente de pelo menos uma potência de base real, positiva e diferente de 1.

Ex.:

5.0 Atividades resolvidas

Questões