1.0 Conceitos iniciais
Um conjunto é uma coleção qualquer de objetos, cada um deles chamado de elemento.
1.1 Representação de um conjunto
Geralmente, nomeamos os conjuntos utilizando letras maiúsculas (por exemplo: A, B, C, D, ..., X,Y, Z) e adotamos letras minúsculas para representar seus elementos (por exemplo: a, b, c, d, ..., x, y, z).
Um mesmo conjunto pode ser representado de várias maneiras, por exemplo:
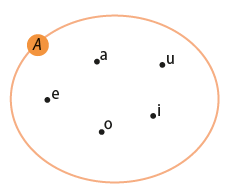
- Os elementos do conjunto são colocados entre chaves e separados por vírgula ou ponto e vírgula: A = {a, e, i, o, u};
- Os elementos do conjunto são indicados por uma ou mais propriedades que os caracterizam: A = {x | x é vogal do nosso alfabeto};
- Os elementos do conjunto aparecem em um diagrama de Venn, como mostra a seguinte imagem:
Para indicar que um elemento faz parte de determinado conjunto, usamos o símbolo ∈ (pertence),
e para indicar que ele não faz parte, usamos o símbolo ∉ (não pertence). Por exemplo, dado o conjunto das vogais A = {a, e, i, o, u}, temos:
i ∈ A (lê-se: i pertence a A);
d ∉ A (lê-se: d não pertence a A).
1.2 Tipos de conjuntos
Quanto ao número de elementos, os conjuntos podem ser classificados como finitos ou infinitos.
Um conjunto é finito quando é possível contar seus elementos. Exemplo do conjunto A das vogais do nosso alfabeto: A = {a, e, i, o, u}. Esse conjunto possui 5 elementos.
OBS: Utilizamos a notação n(A) para indicar a quantidade de elementos do conjunto finito A. Nesse exemplo, temos n(A) = 5.
Um conjunto é infinito quando não é possível contar seus elementos. Por exemplo, dado o conjunto B dos números naturais ímpares: B = {1, 3, 5, 7, 9, ...}
Existem dois conjuntos muito especiais para a Matemática que não: o conjunto unitário e o conjunto vazio.
1.2.1 Conjunto unitário
Um conjunto é unitário quando é formado por um único elemento. Por exemplo:
H = {x | x é um número natural maior do que 6 e menor do que 8};
Como só existe um número natural maior do que 6 e menor do que 8, temos: H = {7}. Logo, H é um conjunto unitário.
1.2.2 Conjunto vazio
O conjunto vazio é aquele que não possui elementos. Ele é representado por { } ou Ø. Por exemplo:
V = {x | x é um número natural menor do que zero}
Como não existe número natural menor do que zero, o conjunto V é vazio. Logo, V = Ø.
Por definição, o conjunto vazio é um conjunto finito.
1.3 Subconjuntos
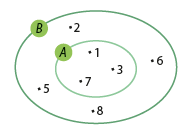
Sejam conjuntos A = {1, 3, 7} e B = {1, 2, 3, 5, 6, 7, 8}, observamos que todo elemento do conjunto A também é elemento de B. Nesse caso, dizemos que A é um subconjunto de B.
De maneira geral:
Um conjunto A é subconjunto de um conjunto B quando qualquer elemento de A também pertence a B.
1.3.1 Está contido ou Contém
Quando um conjunto A é subconjunto de um conjunto B, temos uma relação de inclusão e dizemos que A está contido em B ou, ainda, que A é parte de B. Podemos dizer também que B contém A. Indica-se:
A ⊂ B (lê-se: A está contido em B)
B ⊃ A (lê-se: B contém A)
1.3.2 Conjunto das Partes de um conjunto A (P(A))
O conjunto das partes de um conjunto A é o conjunto de todos os subconjuntos que ele contém, por exemplo:
Seja A = {1,2}. Os Subconjuntos de A são: {1}, {2}, {1,2} e Ø. Então P(A) = {{1}, {2}, {1,2}, Ø}.
Seja B = {a,b,c}. P(B) = {{a}, {b}, {c}, {a,b}, {a,c}, {b,c}, {a,b,c}, Ø}
De uma forma geral, a quantidade de subconjuntos de um conjunto não vazio é 2n, em que n é a quantidade de elementos do conjunto.
1.3.3 Propriedades da relação de inclusão
- Propriedade reflexiva: A ⊂ A, para qualquer A, ou seja, um conjunto sempre é subconjunto dele mesmo.
- Propriedade antissimétrica: Se A ⊂ B e B ⊂ A, então A = B, ou seja, se um conjunto é subconjunto de outro, e vice-versa, então eles são iguais.
- Propriedade transitiva: Se A ⊂ B e B ⊂ C, então A ⊂ C, ou seja, se um conjunto é subconjunto de um segundo, que, por sua vez, é subconjunto de um terceiro conjunto, então o primeiro é subconjunto do terceiro.
OBS:
• A relação de pertinência (x ∈ A) é entre elemento e conjunto, enquanto a relação de inclusão
(A ⊂ B) é entre dois conjuntos.
• Se existir pelo menos um elemento de A que não pertença a B, dizemos que A não está
contido em B ou que B não contém A.
• O símbolo ⊄ significa não está contido.
• O símbolo ⊅ significa não contém.
• O conjunto vazio é subconjunto de qualquer conjunto, ou seja, Ø ⊂ A, qualquer que seja o
conjunto A.
2.0 Igualdade de conjuntos
Analisando os conjuntos A = {vogais da palavra “livro”} e B = {i, o}, observamos que eles possuem exatamente os mesmos elementos. Nesse caso, dizemos que A e B são iguais.
Agora, observe os conjuntos X = {1, 2, 3} e Y = {0, 1, 2, 3}. Como existe um elemento em Y que não pertence a X, dizemos que X e Y são diferentes.
Dois conjuntos são iguais se todos os elementos de um conjunto forem iguais aos elementos do outro conjunto, e vice-versa.
3.0 Atividades resolvidas
4.0 Operações entre conjuntos
4.1 União
A união (também chamada de reunião) de dois conjuntos A e B, que indicamos por A U B, é o conjunto formado pela junção dos elementos que pertencem ao conjunto A com os elementos que pertencem ao conjunto B:
A U B = {x | x ∈ A ou x ∈ B}
Exemplo:
A = {0, 2, 4, 6} e B = {0, 1, 2, 3, 4}; A U B = {0, 1, 2, 3, 4, 6}
Observe que, qualquer que seja o elemento de A U B, ele pertence ao conjunto A ou ao conjunto B ou a ambos.
4.2 Interseção
A intersecção de dois conjuntos A e B, que indicamos por A ∩ B, é o conjunto formado pelos elementos que pertencem a A e também pertencem a B:
A ∩ B = {x | x ∈ A e x ∈ B}
Exemplo:
A = {0, 2, 4, 6} e B = {0, 1, 2, 3, 4}; A ∩ B = {0, 2, 4}
OBS:
Conjuntos A e B que têm interseção vazia (A ∩ B = Ø) são chamados de conjuntos disjuntos.
4.3 Propriedades união e da interseção de conjuntos
A U B = B U A
A ∩ B = B ∩ A
(A U B) U C = A U (B U C)
(A ∩ B) ∩ C = A ∩ (B ∩ C)
A ∩ (B U C) = (A ∩ B) U (A ∩ C)
A U (B ∩ C) = (A U B) ∩ (A U C)
Se A ⊂ B, então A U B = B e A ∩ B = A.
Da mesma maneira, se A U B = B ou A ∩ B = A, então A ⊂ B.
4.4 Quantidade de elementos da união de conjuntos
n(A U B) = n(A) + n(B) - n(A ∩ B)
4.5 Diferença de conjuntos
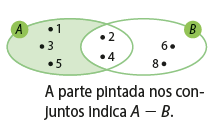
A diferença de dois conjuntos A e B, que indicamos por A - B, nessa ordem, é o conjunto dos elementos que pertencem a A e não pertencem a B:
A - B = {x | x ∈ A e x ∉ B}
Exemplo: dados os conjuntos A = {1, 2, 3, 4, 5} e B = {2, 4, 6, 8},
A - B = {1, 3, 5}
Se B ⊂ A, a diferença A - B é denominada complementar de B em relação a A e é indicada por:
5.0 Exercícios resolvidos
6.0 Conjuntos numéricos
São números usados para contar. Começando por zero e acrescentando sempre uma unidade, obtemos os elementos do conjunto dos números naturais, indicado por N.
N = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, ...}
O conjunto dos números naturais é infinito e podemos representá-lo em uma reta orientada sobre a qual marcamos pontos equidistantes. A cada ponto marcado, fazemos corresponder, ordenadamente, um número natural, e cada número natural é representado por um desses pontos, como mostra a figura a seguir.
A respeito dos números naturais:
- Todo número natural n tem seu sucessor n + 1, que é o número natural que vem imediatamente depois dele. Por exemplo, o sucessor de 5 é 6; o sucessor de 29 é 30.
- O número natural que vem imediatamente antes de um número natural diferente de zero é denominado antecessor. Por exemplo, o antecessor de 10 é 9; o antecessor de 231 é 230.
- Os números naturais n e n + 1 são denominados consecutivos. Analogamente, dizemos que os números naturais n, n + 1, n + 2, ... são consecutivos. Por exemplo, 4 e 5 são consecutivos e 18, 19 e 20 também são consecutivos.
- O subconjunto de N formado por todos os números naturais diferentes de zero é denotado assim:
N* = {1, 2, 3, 4, 5, 6, ...} = N - {0}
6.2 Inteiros
O conjunto formado pelos números positivos, negativos e zero é denominado conjunto dos números inteiros e é representado por Z.
Z = {..., -4, -3, -2, -1, 0, 1, 2, 3, 4, ...}
Todos os números naturais pertencem ao conjunto dos números inteiros, ou seja, o conjunto dos números naturais é um subconjunto do conjunto dos números inteiros, como mostra o diagrama a seguir. Além disso, podemos escrever N ⊂ Z.
A respeito dos números inteiros:
Todo número inteiro tem um antecessor e um sucessor. Por exemplo: o antecessor de -10 é -11, e o sucessor de -1 é 0.
Dois números inteiros são opostos ou simétricos quando a soma deles é igual a zero. Por exemplo: o oposto de 1 é -1, e o oposto de -3 é 3. O oposto de zero é o próprio zero.
números inteiros não nulos: Z* = {..., -4, -3, -2, -1, 1, 2, 3, 4, ...} = Z - {0}
números inteiros não negativos:

números inteiros não positivos:

números inteiros positivos:

números inteiros negativos:

números pares: P = {..., -4, -2, 0, 2, 4, ...}, ou seja, são os números que, divididos por 2, têm resto 0.
números ímpares: I = {..., -3, -1, 1, 3, ...}, ou seja, são os números que, divididos por 2, têm resto 1.
6.3 Racionais
O conjunto dos números racionais, que indicamos por Q, é aquele formado pelos números que podem ser expressos na forma

, sendo
a e
b inteiros e b
≠ 0.

Exemplos: 7 = 7/1 0,6 = 3/5 -0,13 = -13/100 1,333... = 4/3 0,4777... = 43/90
6.3.1 Forma fracionária, forma decimal
Um número racional pode ser representado de duas maneiras: na forma fracionária, como a razão de dois números inteiros, sendo o denominador não nulo; e na forma decimal, que pode ser obtida quando dividimos o numerador pelo denominador que aparecem na forma fracionária. Nesse caso, a parte decimal tem uma quantidade finita de algarismos ou é infinita e periódica.
Para representar, na forma decimal, um número racional escrito como razão de dois números inteiros, dividimos o numerador pelo denominador.
Exemplos: 1/4 = 0,25 14/5 = 2,8 13/6 = 2,1666...
Ao realizar essa divisão, temos duas possibilidades:
O resultado é um número decimal com uma quantidade finita de algarismos depois da vírgula. Nesse caso, temos um número decimal exato. Exemplos: 12/4 = 3 3/4 = 0,75
O resultado é um número decimal com uma quantidade infinita de algarismos depois da vírgula, com um grupo deles se repetindo periodicamente. Nesse caso, temos uma dízima periódica, e o grupo de algarismos que se repetem indefinidamente é chamado de período da dízima.
Exemplos:

(o período é 6)

8.0 Irracionais
Representados por I, são números que
não podem ser escritos na forma

, sendo
a e
b inteiros e b
≠ 0.
Exemplos:
![\sqrt[]{2}\qquad \sqrt[]{3}\qquad \sqrt[]{5}\qquad \pi](https://latex.codecogs.com/svg.image?\sqrt[]{2}\qquad&space;\sqrt[]{3}\qquad&space;\sqrt[]{5}\qquad&space;\pi&space;)
9.0 Reais
É o conjunto formado pela união de todos os conjuntos anteriores: irracionais, racionais, inteiros e naturais.
São subconjuntos do conjunto dos números reais determinados por desigualdades.












Comentários
Postar um comentário