Capítulo 5 - Função Quadrática

Nesta capítulo, você será capaz de:

Esboçar o gráfico de uma função de segundo grau;
Determinar a quantidade de raízes reais de uma função de segundo grau;
Deduzir a "fórmula" de soma e produto das raízes;
Deduzir a forma fatorada de uma função quadrática;
Identificar as coordenadas do vértice de uma parábola;
Identificar o conjunto Imagem;
Esboçar, de fato, a parábola;
Estudar o sinal de uma função de segundo grau;
Resolver inequações de segundo grau.

1.0 Definição

Uma função quadrática, ou função polinomial do segundo grau, ou simplesmente função do segundo grau, é toda função f de Reais em Reais dada por uma lei de formação do tipo f(x) = ax² + bx + c, em que a, b e c pertencem aos Reais e a é diferente de zero.

Veja os exemplos a seguir.

• f(x) = 2x² + 3x + 5, sendo a = 2, b = 3 e c = 5.

• f(x) = 3x² - 4x + 1, sendo a = 3, b = -4 e c = 1.

• f(x) = x² - 1, sendo a = 1, b = 0 e c = -1.

• f(x) = -x² + 2x, sendo a = -1, b = 2 e c = 0.

• f(x) = -4x², sendo a = -4, b = 0 e c = 0.

2.0 Gráfico

São necessários três pontos distintos para se obter a equação de segundo grau que deu origem à função de mesmo grau. Como ainda não conhecemos tais pontos, devemos escolher quantos pontos forem necessários para formar a "cara" da parábola. Esses pontos devem ser obtidos atribuindo valores para x aplicando na lei de formação para então obter um correspondente em y, dessa forma, teremos pares (x,y) que são exatamente os pontos.

EXEMPLO 1

Para construir o gráfico da função f: R → R dada pela lei f(x) = x² + x, atribuímos a x alguns valores (respeitando o domínio da função), calculamos o valor correspondente de y para cada valor de x e, em seguida, ligamos os pontos obtidos:

3.0 Raízes de uma equação do segundo grau

Os números reais x tais que f(x) = 0 são ditos raízes ou zeros da equação quadrática. Em outras palavras, as raízes são os valores de x para os quais y = 0, ou ainda, as soluções (se existirem) da equação ax² + bx + c = 0. Observe a demonstração:

$f(x)=0$
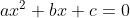
$ax^2+bx+c=0$
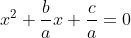
$a(x^2+\frac{b}{a}x+\frac{c}{a})=0$
$x^2+\frac{b}{a}x+\frac{c}{a}=0$
$x^2+\frac{b}{a}x=-\frac{c}{a}$
$x^2+\frac{b}{a}x+\frac{b^2}{4a^2}=\frac{b^2}{4a^2}-\frac{c}{a}$

Perceba que o lado esquerdo da igualdade é um trinômio de quadrado perfeito, e o no lado direito faremos a subtração de frações tirando o M.M.C:

$(x+\frac{b}{2a})^2=\frac{b^2-4ac}{4a^2}$

Extraindo a raiz quadrada em ambos os lados da igualdade, temos:

$x+\frac{b}{2a}=\pm \sqrt{\frac{b^2-4ac}{4a^2}}$
$x=\pm \frac{\sqrt{b^2-4ac}}{2a}-\frac{b}{2a}$

Reorganizando:

$x=\frac{-b\pm \sqrt{b^2-4ac}}{2a}$

Você pode fazer por partes (acredito que ajude no processo de fixação) e chamar de "Delta" o termo dentro da raiz, observe:

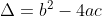
$\Delta =b^2-4ac$

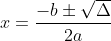
$x=\frac{-b\pm \sqrt{\Delta }}{2a}$

Veja alguns exemplos:

4.0 Quantidade de raízes

As raízes de uma função de segundo grau são os valores x para os quais y = 0, ou seja, são as abscissas dos pontos em que a parábola "corta" o eixo Ox (eixo dos x). Retomemos aos exemplos:

Exemplo 4: o gráfico da função f(x) = x² - 5x + 6 intersecta (corta) o eixo x nos pontos (3,0) e (2,0);

Exemplo 5: o gráfico da função f(x) = 4x² - 4x + 1 intersecta (corta) o eixo x no ponto (1/2,0);

Exemplo 6: o gráfico da função f(x) = 2x² + 3x + 4 não intersecta (não corta) o eixo x.

5.0 Soma e produto (relações de Girard)

Dada uma equação quadrática do tipo ax² + bx + c = 0, com a diferente de zero, é possível determinar o valor da soma (x1 + x2) e do produto (x1.x2) de suas raízes. Sejam x1 e x2 raízes da equação dada, vamos usar de alguns artifícios para demonstrar tais fórmulas. Vejamos:

$x_{1}+x_{2}=\left (\frac{-b+\sqrt{\Delta }}{2a}\right )+\left (\frac{-b-\sqrt{\Delta }}{2a}\right )$

Raiz de delta vai ser anulado, ficando:

$x_{1}+x_{2}=\frac{-2b}{2a}$

$x_{1}+x_{2}=\frac{-b}{a}$

Já o produto:

$x_{1}\cdot x_{2}=\left (\frac{-b+\sqrt{\Delta }}{2a} \right)\cdot \left (\frac{-b-\sqrt{\Delta }}{2a} \right)$

Temos um produto notável no numerador, portanto:

$x_{1}\cdot x_{2}=\frac{(-b)^2-(\sqrt{\Delta })^2}{4a^2}$

$x_{1}\cdot x_{2}=\frac{b^2-{\Delta }}{4a^2}$

Como Delta é igual a:

$\Delta =b^2-4ac$

Substituindo, teremos:

$x_{1}\cdot x_{2}=\frac{b^2-(b^2-4ac)}{4a^2}$

Restando somente

$x_{1}\cdot x_{2}=\frac{4ac}{4a^2}$

Simplificando:

$x_{1}\cdot x_{2}=\frac{c}{a}$

6.0 Forma fatorada

Seja y = f(x) = ax² + bx + c uma função do segundo grau com a diferente de zero, e sejam x1 e x2 raízes reais; então podemos escrevê-la da seguinte forma:

$y=a\left ( x^2+\frac{b}{a}x+\frac{c}{a} \right )$ ou ainda:

$y= a\left [x^2-\left (-\frac{b}{a} \right )x+\frac{c}{a} \right ]$

Sabendo que

$x_{1}+x_{2}=-\frac{b}{a}$

$x_{1}\cdot x_{2}=\frac{c}{a}$

podemos substituir na expressão:

$y=a \left [x^2-\left (x_{1}+x_{2} \right )x+x_{1}\cdot x_{2} \right ]$

Desenvolvendo:

$y=a \left [x^2- x_{1}\cdot x-x_{2}\cdot x +x_{1}\cdot x_{2} \right ]$

Colocando os (x - x1) em evidência:

$y=a \left [x(x- x_{1})-x_{2} (x -x_{1}) \right ]$

Colocando em evidência mais uma vez, e eis a forma fatorada.

$y=a \left [(x- x_{1})\cdot (x -x_{2}) \right ]\\\\ y=a (x- x_{1})\cdot (x -x_{2})$

Confira um exemplo

7.0 Coordenadas do vértice da parábola

Chamemos de vértice da parábola o ponto mais abaixo dela (para a > 0), ou mais acima dela (para a < 0). Esse ponto denotamos pela letra V. Seja V, o vértice da parábola, de coordenadas xv e yv; e x1 e x2 as raízes de uma função qualquer, observa-se que a coordenada xv (lê-se "x do vértice) é ponto médio do seguimento x1x2, ou seja, situa-se exatamente no meio das duas raízes (para o caso de Δ > 0). Veja a figura:

7.1 Coordenada x do vértice

Se xv é ponto médio dos seguimento x1x2, então é possível determiná-lo pela média aritmética de x1 e x2. Vejamos:

$x_{v}=\frac{x_{1}+x_{2}}{2}$

Sabendo que

$x_{1}=\frac{-b+ \sqrt{\Delta }}{2a} \\\\ x_{2}=\frac{-b- \sqrt{\Delta }}{2a}$

Substituindo na primeira expressão teremos:

$x_{v}=\frac{\frac{-b+ \sqrt{\Delta }}{2a}+\frac{(-b- \sqrt{\Delta })}{2a}}{2}$

2a é denominador comum, portanto, basta somar no numerador maior:

$x_{v}=\frac{\frac{-b+ \sqrt{\Delta }-b-\sqrt{\Delta }}{2a}}{2}\\\\\\x_{v}=\frac{\frac{-2b}{2a}}{2}$

Uma fração "dentro" de outra, aplica-se, então, a regra do R.I. (Repete a 1ª e a multiplica pelo Inverso da 2ª):

$x_{v}=\frac{-2b}{2a}\cdot \frac{1}{2}\\\\\\x_{v}=\frac{-2b}{4a}$

Eis a coordenada x do vértice:

$x_{v}=\frac{-b}{2a}$

7.2 Coordenada y do vértice

A coordenada y do vértice é simplesmente a imagem da coordenada x do vértice, ou seja:

$y_{v}=f\left ( x_{v} \right )$

Como

$x_{v}=\frac{-b}{2a}$

Substituindo:

$y_{v}=f\left ( \frac{-b}{2a} \right )$

Agora, substituindo na função genérica [f(x) = ax² + bx + c], teremos:

$y_{v}=f\left ( \frac{-b}{2a} \right )= a\left (\frac{-b}{2a} \right )^{2}+b\left (\frac{-b}{2a} \right )+c$

Desenvolvendo:

$y_{v}= \frac{ab^2}{4a^2} -\frac{b^2}{2a} +c$

Tirando o M.M.C

$y_{v}= \frac{ab^2-2ab^2+4a^2c}{4a^2}$

Resolvendo:

$y_{v}= \frac{-ab^2+4a^2c}{4a^2}$

Colocando a em evidência:

$y_{v}= \frac{a\left (-b^2+4ac \right )}{4a^2}$

Como a é diferente de zero, podemos simplificar:

$y_{v}= \frac{-b^2+4ac }{4a}$

Colocando -1 em evidência:

$y_{v}= \frac{-\left (b^2-4ac \right )}{4a}$

Apareceu um termo muito conhecido nosso: Δ = b² - 4ac; ao substituir teremos a expressão para o y do vértice:

$y_{v}= -\frac{\Delta }{4a}$

8.0 O conjunto imagem de uma função de segundo grau

É o conjunto de todos os valores que y pode assumir. Como vimos, para a > 0, tem-se concavidade voltada para cima, e o vértice limita inferiormente a função, ou seja, é ponto de mínimo. O conjunto imagem, nesse caso, é y ≥ yv. Escreve-se formalmente:

$Im=\left \{ y\epsilon \mathbb{R}|y\geq y_{v} \right \}$

Substituindo:

$Im=\left \{ y\epsilon \mathbb{R}|y\geq -\frac{\Delta }{4a} \right \}$

a > 0

Para a < 0, tem-se concavidade voltada para baixo, e o vértice limita superiormente a função, ou seja, é ponto de máximo. O conjunto imagem, nesse caso, é y ≤ yv. Formalmente:

$Im=\left \{ y\epsilon \mathbb{R}|y\leq -\frac{\Delta }{4a} \right \}$

a < 0

9.0 O termo independente de uma equação quadrática

O termo independente, ou seja, o termo que não depende de variável alguma na função de segundo grau foi definido como sendo o c. Na função genérica f(x) = ax² + bx + c, se fizermos x = 0, descobriremos o ponto pelo qual o gráfico intersecta (corta) o eixo Oy. Vejamos:

$f(0)=a\cdot 0^2+b\cdot 0+c \\ f(0)=c$

O gráfico de uma função de segundo grau passa sempre pelo ponto (0,c). Retornemos ao exemplo 5:

f(x) = 4x² - 4x + 1

Observe que o termo c = 1, então o gráfico intersecta o eixo Oy nesta ordenada, portando, passa pelo ponto (0,1)

10.0 Esboço da parábola (agora com os pontos mais importantes)

Aprendemos a calcular as raízes (se existirem), que são os pontos onde o gráfico intersecta (corta) o eixo Ox; aprendemos a calcular as coordenadas do vértice; identificamos o ponto de intersecção com o eixo Y. Agora temos todos os pontos ditos "mais importantes" para esboçar com mais qualidade o gráfico desse tipo de função. Exemplo:

OBS: Como vimos, quando se tem duas raízes distintas (Δ > 0), a coordenada x do vértice é a média aritmética das duas raízes. As raízes são 1/2 e 2, portanto, o x do vértice será:

${x_{v}=}\frac{\frac{1}{2}+2}{2} \\ x_{v}=\frac{5}{4}$

Observe também que a reta que passa pelo vértice e é paralela ao eixo Oy é o eixo de simetria da parábola.

Vejamos outro exemplo:

OBS: Quando se tem uma raiz dupla (Δ = 0), esta coincide com vértice da parábola.

Mais um exemplo:

OBS: Quando não se tem raízes reais (Δ < 0), temos que escolher mais pontos; preferencialmente pontos equidistantes (mesma distância) horizontalmente do vértice para formar a "cara" da parábola.

Vejamos agora um exemplo em que se dá o gráfico da parábola com alguns pontos e se pede a equação dela:

11.0 Estudo do sinal de uma função de segundo grau

Seja f: R → R uma função genérica do segundo grau tal que f(x) = ax² + bx + c. Temos três casos:

11.1 (Δ > 0)

A função assume duas raízes reais distintas (x1 ≠ x2); e a parábola intersecta o eixo Ox em dois pontos distintos (as próprias raízes).

Observe que para a > 0, qualquer valor que tomemos para x que seja menor que x1 nos dará valores sempre positivos para y, ou seja, a função é positiva para x < x1. Note que se tomarmos valores para x maiores que x2, teremos sempre valores positivos para y também, ou seja, a função também é positiva para x > x2.

Perceba que se tomarmos valores para x maiores x1 e menores que x2, teremos valores negativos para y, ou seja, a função é negativa para x1 < x < x2.

O contrário acontecerá para quando a < 0. Observemos:

Para a < 0, qualquer valor que tomemos para x que seja menor que x1 nos dará valores sempre negativos para y, ou seja, a função é negativa para x < x1. Se tomarmos valores para x maiores que x2, teremos sempre valores negativos para y também, ou seja, a função também é negativa para x > x2.

Se tomarmos valores para x maiores que x1 e menores que x2, teremos valores positivos para y, ou seja, a função é positiva para x1 < x < x2.

11.2 (Δ = 0)

A função assume duas raízes iguais (x1 = x2); e a parábola intersecta o eixo Ox em apenas um ponto (a própria raiz dupla que coincide com o próprio vértice).

Observe que para a > 0, qualquer valor que tomemos para x que seja menor x1 ou maior x2 (lembrando que x1 = x2) nos dará sempre valores positivos para y, ou seja, a função é positiva para x ≠ x1 e x ≠ x2. Note também que nesse caso y não assume valores negativos, ou seja, y ≥ 0 para qualquer x pertencente ao domínio da f.

Observe que para a < 0, qualquer valor que tomemos para x que seja menor x1 ou maior x2 (lembrando que x1 = x2) nos dará sempre valores negativos para y, ou seja, a função é negativa para x ≠ x1 e x ≠ x2. Note também que nesse caso y não assume valores positivos, ou seja, y ≤ 0 para qualquer x pertencente ao domínio da f.

11.3 (Δ < 0)

A função não admite raízes reais; a parábola não intersecta o eixo Ox; e o sinal é o indicado nas figuras: