Capítulo 7 - Função Exponencial

Neste capítulo, você

Relembrará conceitos de potenciação e radiciação;
Definirá potência de expoente negativo e racional;
Relembrará as propriedades de potenciação e radiciação;
Verá "a cara" do gráfico de uma função exponencial;
Será capaz de resolver equações exponenciais.

1.0 Potência de expoente natural

$a^{n}$

a = base

n = expoente

1.1 Propriedades

$a^{n}\cdot a^{m}=a^{n+ m} \\\\ \frac{a^{m}}{a^{n}}=a^{m-n}\\\\\left ( a\cdot b \right )^{n}=a^{n}\cdot b^{n}\\\\\left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}\left ( b\neq 0 \right )\\\\\ \left (a^{m} \right )^{n}=a^{m\cdot n}$

2.0 Potência de expoente inteiro negativo

$a^{-n}=\frac{1}{a^{n}}$

As propriedades do item 1.1 valem para potências de expoente inteiro negativo.

3.0 Raiz n-ésima

$\sqrt[n]{a}=b <=> b^{n}=a\\\forall b\geqslant 0$

logo:

$\left (\sqrt[n]{a} \right )^{n}=a$

4.0 Propriedades

$\sqrt[n]{a^{m}}=a^{\frac{m}{n}}$ (Quem está na sombra vai para o sol, quem está no sol vai para a sombra);

$\sqrt[n]{a\cdot b}=\sqrt[n]{a}\cdot \sqrt[n]{b}\\\\\sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\left (b\neq 0 \right )\\\\\\\left ( \sqrt[n]{a} \right )^{m}=\sqrt[n]{a^{m}}\\\\\sqrt[p]{\sqrt[n]{a}}=\sqrt[p\cdot n]{a}$

5.0 Função exponencial

É toda função de Reais em Reais estritamente positivos dada por uma lei na forma

$f(x)=a^{x}$

em que a é um número real conhecido, desde que a > 0 e a ≠ 1.

Exemplos:

$y = \left ( \frac{1}{2} \right )^{x}\\\\f(x)=3^{x}$

5.1 Gráfico de função exponencial

5.1.1 Propriedades

Na função exponencial cuja lei é 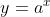$y=a^{x}$ , em que a ≠ 0, observamos que para x = 0, y = 1. Isso significa que o gráfico da função 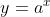$y=a^{x}$ intersecta (corta) o eixo Oy no ponto de ordenada 1.

Se a > 1, então o gráfico será crescente. Observe-o:

As funções a seguir são crescentes: $y=2^{x}; y=3^{x};y=e^{x}$ .

se 0 < a < 1, então o gráfico será decrescente. Veja

As funções a seguir são decrescentes: $y=\left (\frac{1}{2} \right )^{x}; y=\left (\frac{1}{3} \right )^{x};y=\left (\frac{1}{10} \right )^{x}$

Como se pode observar nos gráficos, em qualquer cenário (seja a > 0, ou 0 < a < 1) o gráfico da função exponencial nunca intersectará (cortará) o eixo Ox, ou seja, não existe x tal que y seja menor ou igual a zero. Essa constatação nos permite escrever o conjunto imagem desse tipo de função:

$Im=\left \{ y \ \epsilon \ \mathbb{R}|y>0 \right \}=\mathbb{R}_{+}^{*}$ (Reais estritamente positivos).

6.0 Equação exponencial

Definição: uma equação exponencial é aquela que apresenta a incógnita no expoente de pelo menos uma de suas potências.

São equações exponenciais: $4^{x}=8;\left (\frac{1}{9} \right )^{x}=81 \ e \ 9^{x}-3^{x}=72$ .

O método mais imediato de resolução de equações desse tipo é de igualar as bases em ambos os lados da equação, por exemplo:

$4^{x}=8;\\\left (2^{2} \right )^{x}=2^{3}\\2^{2x}=2^{3}$

Bases iguais, expoentes iguais. Daí se tira que 2x = 3, portanto, x = 3/2; x = 1,5.

Confira a resolução de alguns exercícios propostos para esse capítulo clicando aqui

7.0 Aplicações

Meia vida e Radioatividade

Decaimento radioativo

O núcleo de um átomo com excesso de energia tende a se estabilizar emitindo um grupo de partículas (radiação alfa ou beta) ou ondas eletromagnéticas (radiações gama). Em cada emissão de uma das partículas, há variação do número de prótons e nêutrons no núcleo e, deste modo, um elemento químico se transforma em outro. O processo pelo qual se dá a emissão dessas partículas é chamado de decaimento radioativo.

Meia-vida

Considerando uma grande quantidade de átomos de um mesmo elemento químico radioativo, espera-se certo número de emissões por unidade de tempo. Essa “taxa de emissões” é a atividade da amostra. Cada elemento radioativo se transmuta (desintegra) a uma velocidade que lhe é característica. Meia-vida é o intervalo de tempo necessário para que a sua atividade radioativa seja reduzida à metade da atividade inicial. Após o primeiro período de meia-vida, a atividade da amostra se reduz à metade da atividade inicial; passado o segundo período, a atividade se reduz a 1/4 da atividade inicial e assim por diante, como mostra o gráfico abaixo.

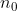A lei que define essa função exponencial é $n(x)=\frac{n_{0}}{2^{x}}$ , sendo x a quantidade de meias-vidas, $n_{0}$ o número de átomos correspondente à atividade inicial e n(x) o número de átomos em atividade após x meias-vidas. Exemplo de meia-vida: O iodo-131 é um elemento químico radiativo, usado na Medicina Nuclear, em exames e tratamentos de tiroide, e tem meia-vida de 8 dias. Isso significa que, em 8 dias, metade dos átomos deixarão de emitir radiação.

Exemplos de elementos radioativos:

Fonte de pesquisa: Energia nuclear e suas aplicações. Disponível em: <www.cnen.gov.br/images/cnen/documentos/educativo/apostila-educativa-aplicacoes.pdf>.

Acesso em: 4 mar. 2016.

Confira a resolução de alguns exercícios propostos para esse capítulo clicando aqui

Pesquisar este blog

Matemática ECIT-JP

Capítulo 7 - Função Exponencial

Comentários

Postar um comentário

Postagens mais visitadas deste blog

[Vol. 2] Capítulo 02 - Função exponencial

[Vol. 5] Cap. 01 - Áreas de figuras planas

[Vol. 1] Capítulo 01 - Conjuntos