Capítulo 8 - Função logarítmica

 Neste capítulo, você irá

• Definir um logaritmo;
• Conhecer o logaritmo decimal e o natural (neperiano);
• Conhecer as propriedades (produto; quociente; potência; mudança de base);
• Definir a função logarítmica;
• Esboçar o gráfico de uma função logarítmica;
• Ver a relação entre a função logarítmica e a função exponencial;
• Conhecer as propriedades do gráfico da função logarítmica;
• Resolver equações exponenciais aparentemente "irresolvíveis".

1.0 Definição

Sendo a e b números reais e positivos, com a ≠ 0, chamaremos logaritmo de b na base a o expoente  ao qual se deve elevar a base a de modo que a potência 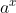 seja igual a b.

Em que

• a é a base do logaritmo;
• b é o logaritmando;
• x é o próprio logaritmo.

1.1 Convenção 

Convencionou-se omitir a base do logaritmo quando esta for 10, portanto, o logaritmo de base 10 pode ser escrito sem base.

1.2 Consequências

Sejam a, b e c números reais com a > 0, b > 0, c > 0 e a ≠ 1. Será consequência da definição:

• o logaritmo de 1 em qualquer base a é igual a 0; 

• o logaritmo de a na base a é igual a 1;

• a potência de base a e expoente  é igual a b.

• se dois logaritmos de mesma base são iguais, então os logaritmandos também são iguais. Da mesma forma que se dois números reais positivos são iguais, seus logaritmos de mesma base também são iguais;

2.0 Logaritmo neperiano (ou logaritmo natural)

É um logaritmo cuja base é o número e (número de Euler). Convencionou-se escrever "ln x" para representar os logaritmos naturais:

3.0 Propriedades

3.1 Logaritmo do produto

Em qualquer base maior do que zero e diferente de 1, o logaritmo do produto é igual a soma dos logaritmos:

3.2 Logaritmo do quociente

Em qualquer base maior do que zero e diferente de 1, o logaritmo do quociente é igual a diferença dos logaritmos:

3.3 Logaritmo da potência (no logaritmando) 

Em qualquer base maior do que zero e diferente de 1, o logaritmo de uma potência de base real e positiva é igual ao produto do expoente pelo logaritmo da base da potência:

3.4 Logaritmo da potência (na base)

3.5 Mudança de base

Sejam a, b e c reais positivos, com a e b diferentes de 1. É verdade que:

3.5.1 Consequência da mudança de base

Sejam a e b reais positivos e diferentes de 1. Também é verdade que:

4.0 Função logarítmica 

Dado um número real a (a > 0, a ≠ 1), chamaremos de função logarítmica de base a a função f de 

 em  (Reais estritamente positivos em Reais) dada pela lei 

Uma função dessa natureza associa cada número real positivo a seu logaritmo na base a.

Exemplo

4.1 Gráfico de uma função logarítmica

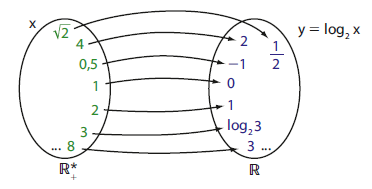
Construamos o gráfico da função f, com domínio 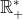, definida por  Para isso, façamos uma tabela atribuindo valores convenientes para x e obtendo valores correspondentes para y.

Observações:

• o gráfico da f está inteiramente contido nos quadrantes 1 e 4, pois a função só está definida para x > 0 (vide o domínio);
• o conjunto imagem de f é R.

Clique para ver os exercícios e resolução de alguns deles