[Vol. 2] Capítulo 1 - A circunferência Trigonométrica

 Neste capítulo, você será irá:

• Medir arcos e ângulos;
• Definir a Circunferência Trigonométrica;
• Conhecer as simetrias para reduzir arcos ao primeiro quadrante.
  

1.0 Arcos e ângulos

Seja uma circunferência de centro O, tomemos sobre ela dois pontos distintos A e B. A circunferência ficou dividida em duas partes, cada uma chamada de arco de circunferência.

Observe que a todo arco  corresponde um ângulo central, ou seja, um ângulo cujo vértice é o centro da circunferência.

1.1 Medida e comprimento de Arco

A medida angular de um arco ou, simplesmente, a medida de um arco é igual à medida do ângulo central correspondente. Veja os exemplos:

A medida linear de um arco refere-se ao seu comprimento. É como se estivéssemos medindo o arco com uma fita métrica.

1.1.1 Unidades de medida de arcos e ângulos

Medida de arco: grau (°) ou radiano (rad);

Grau: dividiu-se a circunferência em 360 partes, cada parte corresponde a um grau;

Radiano: É a medida do arco cujo comprimento é igual ao raio da circunferência.

 

 Como sabemos, o comprimento C  de uma circunferência de raio r é igual a 2πr. Isso significa que o raio da circunferência cabe 2π vezes no comprimento dela (aproximadamente 6,28 vezes). Assim, um arco de circunferência de comprimento igual a r mede 1 rad; um arco de comprimento igual a 2r mede 2 rad etc. Seguindo o mesmo princípio, uma circunferência de comprimento 2πr (uma volta completa) mede 2πr rad (que corresponde a 360°). Então:

A associação em destaque é mais simples e será usada daqui em diante.

Exercícios resolvidos

1.1.2 O comprimento de um arco

 Em geral podemos dizer que:

Exercícios resolvidos:

2.0 A Circunferência Trigonométrica

Vamos fixar dois eixos perpendiculares cruzando-se em O. No sistema descrito, vamos considerar uma circunferência com centro em O e raio unitário (uma unidade de comprimento). 

O círculo limitado por essa circunferência ficou dividido em quatro quadrantes (1ºQ, 2ºQ, 3ºQ, 4ºQ). 

Por convenção, os arcos que serão tomados nessa circunferência devem começar no ponto A (1,0) - interseção da circunferência com o semieixo horizontal positivo. O sentido dos arcos deve ser o seguinte: anti-horário é positivo, horário é negativo.  

2.1 Simetrias 

Na circunferência trigonométrica, teremos três tipos de simetria: em relação ao eixo vertical, em relação ao eixo horizontal e em relação ao centro.

Simetria em relação ao eixo vertical:

Seja p o ponto final do arco, o simétrico de p em relação ao eixo vertical é o ponto p' . Os ângulos que aparecem descritos na imagem são congruentes.

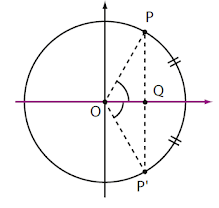
Simetria em relação ao eixo horizontal:

Seja p o ponto final do arco, o simétrico de p em relação ao eixo vertical é o ponto p' . Os ângulos que aparecem descritos na imagem são congruentes.

Simetria em relação ao centro:

Seja p o ponto final do arco, o simétrico de p em relação ao eixo vertical é o ponto p' . Os ângulos que aparecem descritos na imagem são congruentes.