[Vol. 2] Capítulo 03 - Função Logarítmica
1.0 Motivação
O que acontece quando não podemos escrever ambos os lados da igualdade como potências de mesma base? Por exemplo ?
Para isso, utiliza-se o conceito de logaritmo.
2.0 Logaritmo
Sejam a e b números reais positivos, com a ≠ 1. O logaritmo de b na base a é o expoente x tal que :
- b é o logaritmando
- a é a base
- x é o logaritmo de b na base a
Exemplos:
d) Calcular
2.1 Propriedades da definição de logaritmo
Sendo a, b, c são números reais e positivos, a ≠ 1 e m ∈ R valem as seguintes propriedades:
2.2 Logaritmo decimal
É o logaritmo cuja base é 10. Pode-se omitir sua base.
Por exemplo: pode ser escrito simplesmente como
.
2.3 Logaritmo Natural (ou Neperiano)
É o logaritmo cuja base é o número e ( aproximadamente 2,71). Tem uma simbologia própria:
3.0 Atividades resolvidas
Exercícios
4.2 Logaritmo do quociente:
4.3 Logaritmo de uma potência
4.4 Mudança de base
Vejamos uma propriedade que permite mudar a base de um logaritmo:
Exercícios
É possível aplicar logaritmo em ambos os lados de uma igualdade a fim de desenvolver certas equações e inequações, por exemplo:
6.1 Gráfico de uma função logarítmica
Note que as curvas dos gráficos se aproximam do eixo y, mas nunca o tocam
6.3 Relação entre a função exponencial e a função logarítmica
a, b, c positivos e a diferente de 1.
7.0 Equações logarítmicas
São equações que apresentam a incógnita no logaritmando ou na base de um logaritmo de base real positiva e diferente de 1. Para resolver, basta utilizar a definição de logaritmo ou a propriedade anteriormente vista:
8.0 Inequações logarítmicas
São desigualdades que apresentam incógnita no logaritmando ou na base de um logaritmo de base real positiva e diferente de 1.
ATENÇÃO
Assim como nas inequações exponenciais, nas inequações logarítmicas devemos observar se a base é maior do que 1 ou se está entre 0 e 1 para manter ou não o sinal da desigualdade:
9.0 Exercícios
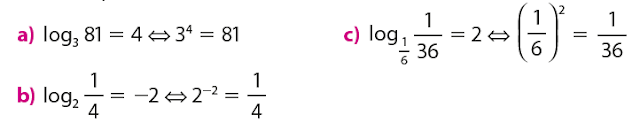
Comentários
Postar um comentário