[Vol. 5] Cap. 03 - Poliedros

 1.0 Definição

São sólidos formados por um número finito de polígonos e pela região do espaço limitada por eles, em que: 

• cada lado desses polígonos é comum a dois, e somente dois, polígonos;
• a intersecção de quaisquer dois polígonos é um lado comum ou um vértice comum ou é vazia.

1.1 Componentes

• faces: são os polígonos que formam a superfície do poliedro;
• arestas: são os lados comuns a duas faces do poliedro;
• vértices: são os vértices das faces do poliedro.

1.2 Nomenclatura

1.3 Poliedros convexos e não convexos

Em um poliedro, se qualquer reta, não paralela a nenhuma das faces, intersecta suas faces

em, no máximo, dois pontos, dizemos que ele é convexo; caso contrário, é um não convexo.

Exemplos

1.4 Relação de Euler

Seja

F = número de faces;

A = número de arestas;

V = número de vértices.

Segue que: 

Exemplos

2.0 Poliedros regulares

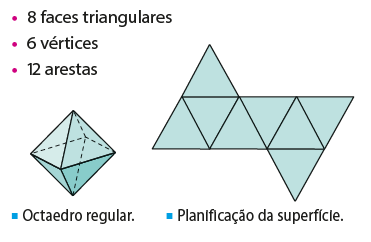
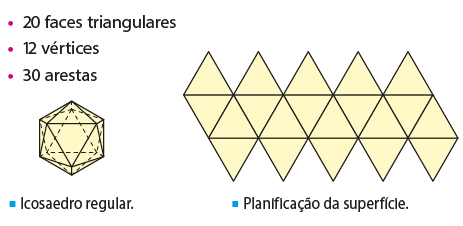
São poliedros cujas faces são polígonos regulares e congruentes entre si e quando em todos os vértices concorre o mesmo número de arestas. São apenas cinco poliedros regulares: tetraedro, hexaedro, octaedro, dodecaedro e icosaedro.

Exercícios

3.0 Prismas

3.1 Prisma Regular

Se o prisma for reto e as bases forem polígonos regulares, o prisma é dito regular.

3.2 Paralelepípedos

É um prisma cujas bases são paralelogramos.

• Paralelepípedo reto retângulo ou bloco retangular: é um prisma reto cujas bases e faces laterais são retângulos. O paralelepípedo reto retângulo é um caso particular do paralelepípedo.

• Cubo ou hexaedro regular: é um prisma reto cujas faces são todas quadradas. O cubo é um caso particular do paralelepípedo reto retângulo.

3.3 Secção transversal de um prisma

A intersecção de um prisma com um plano paralelo às suas bases é denominada secção transversal do prisma. Observe na figura que a secção transversal de um prisma é um polígono congruente aos polígonos das bases.

3.4 Área da superfície de um prisma

Em um prisma, definimos:

• área da base (Sb) como a área de um dos dois polígonos que formam as bases;

• área lateral (Sl) como a soma das áreas de todas as faces laterais;

• área total (St) como a soma da área lateral e das áreas das bases.

Assim, podemos escrever:

Atividades resolvidas

3.5 Volume de um prisma

Em que: 

Sb = Área da base  

h = altura.

 No caso de um paralelepípedo reto retângulo, temos: 

No caso de um cubo: 

Exercícios:

4.0 Pirâmides

4.1 Área da superfície de uma pirâmide

4.2 Volume de uma pirâmide

4.2.1 atividades resolvidas

Exercícios